HISAT2 (Hierarchical Indexing for Spliced Alignment of Transcripts 2) is a graph-based read mapping tool for both DNA and RNA sequences.
HISAT2 enables a fast search through its graph index, mapping reads to the entire human genome along with a large number of variants. Since it is a widely used tool, at PetaGene we have added it to our test suite to ensure our compressed files and transparent decompression technology work optimally with HISAT2.
In this blog post we demonstrate the compatibility of PetaGene software with HISAT2, showing benefits such as faster transfer and shorter analysis times as a result of working with compressed data.
To test HISAT2 with PetaGene’s software, we losslessly compressed paired, FASTQ.gz reads from an RNA-seq experiment using PetaSuite Cloud Edition (CE). PetaSuite CE is able to write files directly to cloud storage. In this example, the files are compressed and streamed directly to an AWS S3 bucket created for this study.
$ time petasuite --compress --md5match --validation md5full \
--species auto ERR1138635_1.fastq.gz ERR1138635_2.fastq.gz \
--dstpath s3://demo_hisat/hisat2_testfiles/compressed
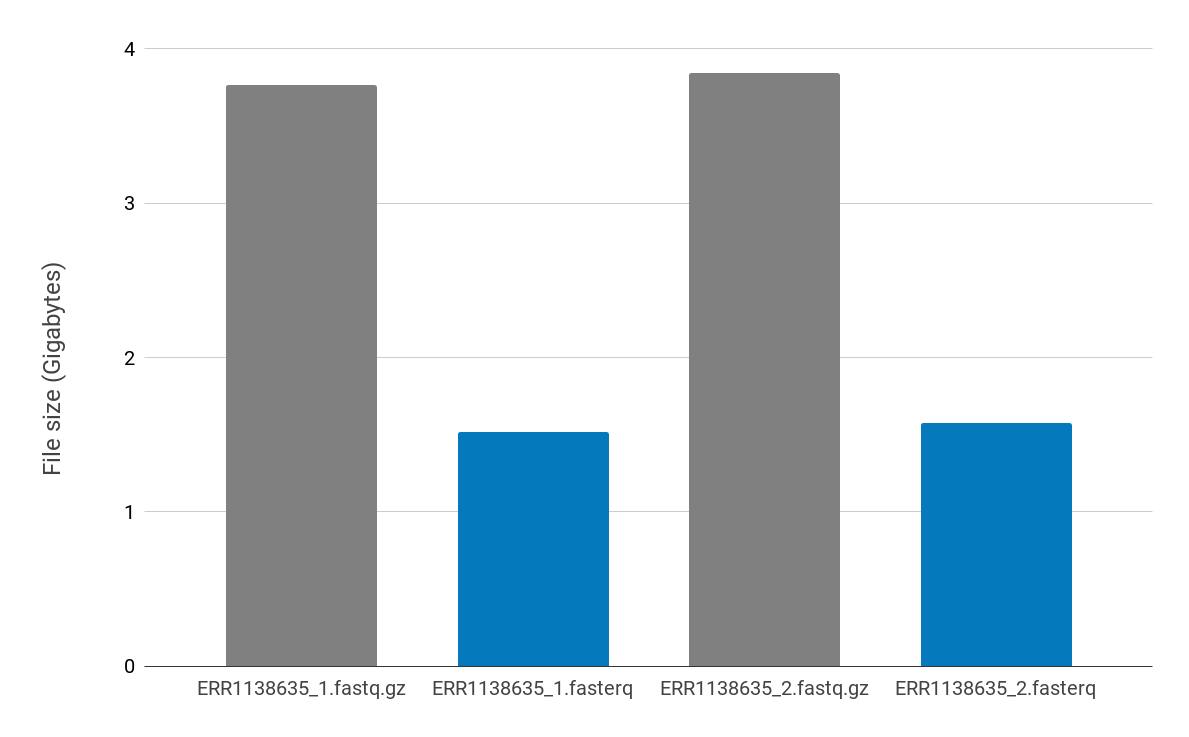
The PetaSuite compressed data are used as the input into HISAT2. To do this the PetaLink decompression library needs to be loaded. PetaLink transparently handles decompression of the compressed files, serving original uncompressed data to HISAT2. With the PetaLink library loaded, virtual, uncompressed files are inserted into the filesystem (shown below in blue). These virtual files look and behave exactly as the original uncompressed file would, but the virtual files do not consume any inode resources.
$ LD_PRELOAD=/usr/lib/petalink.so bash # load petalink
$ ls -lh s3://demo_hisat/hisat2_testfiles/compressed
ERR1138635_1.fasterq
ERR1138635_1.fastq.gz -> ERR1138635_1.fasterq.#.fastq.gz
ERR1138635_2.fasterq
ERR1138635_2.fastq.gz -> ERR1138635_2.fasterq.#.fastq.gz
By default, we present virtual files as FASTQ.gz files. However, HISAT2 takes unzipped FASTQ files as the input, normally performing an unzip step if a FASTQ.gz file is used. With PetaSuite-compressed files, it is possible to have each compressed file presented back as multiple different virtual files by simply setting an environment variable. Below, we set the environment variable to generate a virtual FASTQ file. Thus one FASTERQ file can be presented as multiple different virtual files.
$ export PetaLinkMode=+fastq
$ ls -lh s3://demo_hisat/hisat2_testfiles/compressed
ERR1138635_1.fasterq
ERR1138635_1.fastq -> ERR1138635_1.fasterq.#.fastq
ERR1138635_1.fastq.gz -> ERR1138635_1.fasterq.#.fastq.gz
ERR1138635_2.fasterq
ERR1138635_2.fastq -> ERR1138635_2.fasterq.#.fastq
ERR1138635_2.fastq.gz -> ERR1138635_2.fasterq.#.fastq.gz
These virtual files can be used directly with HISAT2, e.g.:
$ export PetaLinkMode=+fastq
$ hisat2 -x grch38/genome \
-1 s3://demo_hisat/hisat2_testfiles/compressed/ERR1138635_1.fastq \
-2 s3://demo_hisat/hisat2_testfiles/compressed/ERR1138635_2.fastq
Compressing files using PetaGene’s technology offers a number of benefits. The smaller size means the cost of storing the data is lower. Additionally, transferring the data between storage and computing nodes is faster, reducing I/O bottlenecks. Furthermore, PetaLink ensures transparent, fast access of compressed data to existing tools and workflows without any modifications.
Here, we carried out a series of benchmarks showing that HISAT2 works with our compressed files and the transparent decompression library, giving performance improvements in the speed of transfer and analysis.
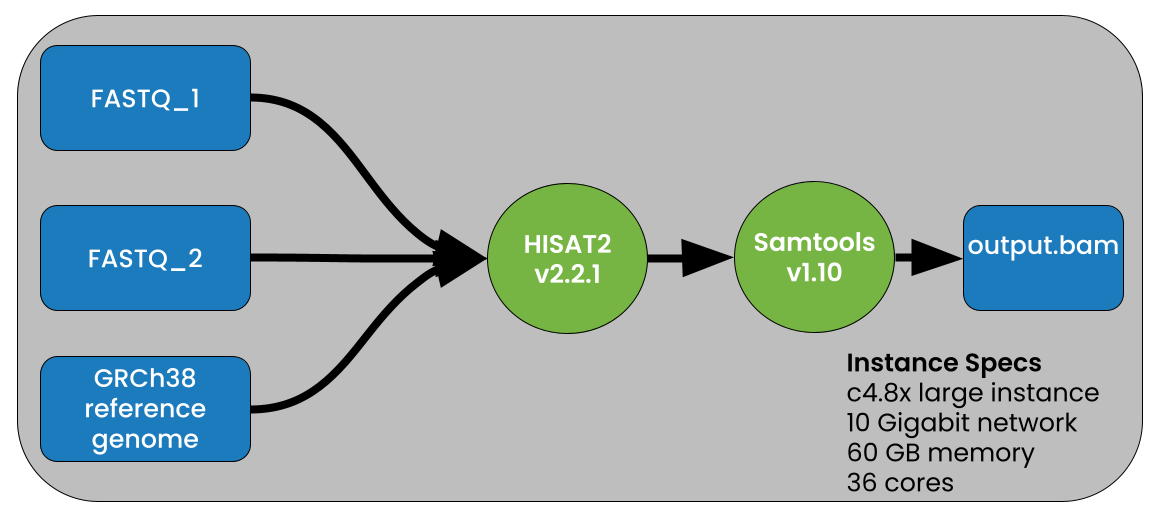
To test the performance gains when using compressed vs uncompressed data we used the pipeline shown in Figure 2.
Results
1. PetaGene-compressed files transparently work with HISAT2.
This demo shows that PetaGene compressed files can be used as input into HISAT2 using the PetaLink library to perform transparent decompression to serve original, uncompressed data to HISAT2. The subsequent output data is in the SAM format, and so, to generate a BAM file, we piped the output to samtools (samtools sort -@ 8 -O BAM -o output.bam) as shown in Figure 2.
2. Runtime is shorter when using PetaGene compressed files.
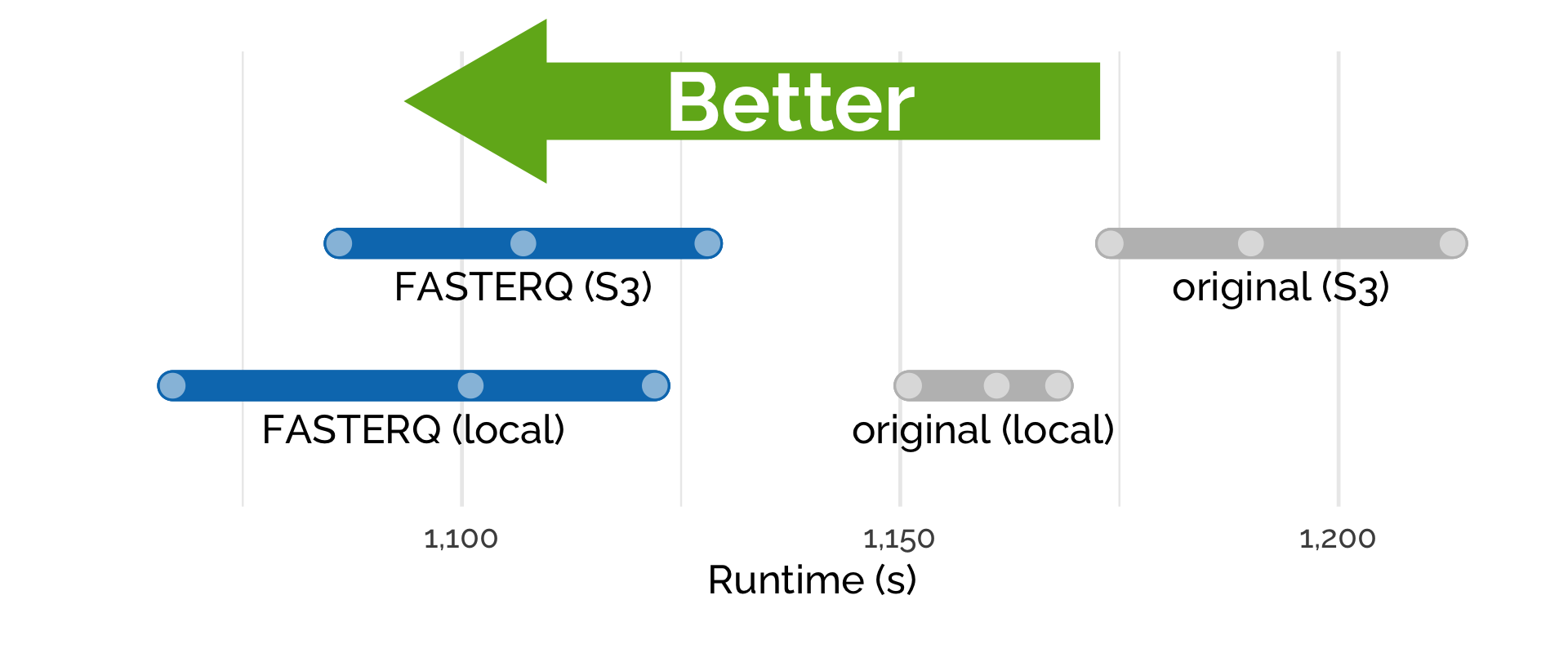
When executing the pipeline, we measured the time it took to process the samples when the data was stored locally on the instance or by directly streaming the data from S3 (Figure 3). In both scenarios, using compressed files sped up the analysis with shorter runtimes recorded. Importantly, PetaLink Cloud Edition carries out transparent, just-in-time decompression and allows streaming data directly from S3.
3. Streaming directly from the cloud removes the need for local storage on the instance.
By streaming the data directly from S3 using PetaLink, we didn’t need to attach large storage to the compute instance.
4. PetaLink allows HISAT2 to take input files that are stored in the cloud.
Furthermore, PetaLink enables HISAT2 to work with data stored in cloud/object storage (AWS, GCP, Azure and any S3-compliant object storage) without any need to modify HISAT2.
PetaLink technology enables:
Cloud-enabling technology — allowing tools to natively work with data stored in the cloud.
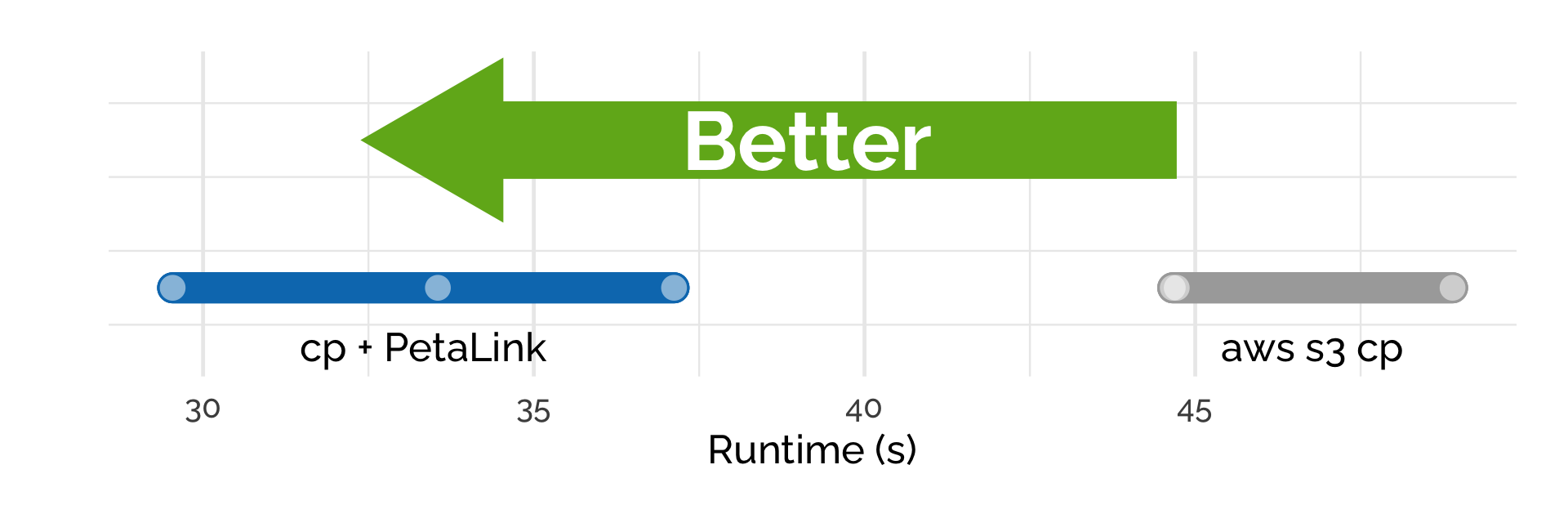
With the PetaLink library loaded, standard cp can be used to copy files directly from cloud storage to the instance. Here we copied the paired, FASTQ.qz files (7.62 GB) from S3 to the C4.8x large instance, which has a 10 gigabit network connection. We used the standard Linux cp binary and the aws s3 cp command-line tool.
High-speed transfer of data
Using cp + PetaLink saw a speedup of 40% on average, with the average speed of transfer 1.85 Gbps compared to 1.32 Gbps for aws s3 cp.
Summary
PetaGene offers bioinformatics users lossless compression software that helps to reduce storage costs and accelerate data transfer and analysis.
-
- PetaGene reduced the storage costs by 60%, reduced the transfer time for uncompressed data by 40%, reduced the transfer time for compressed data by 76%, and reduced the analysis time by about 7%.
-
- Using our PetaLink library, decompression of the files is handled transparently, meaning that compressed files can be used for day-to-day analysis as PetaLink ensures that all tools and applications see original, uncompressed data. The analysis runs faster when the compressed data is used as input in this way.
-
- PetaLink Cloud has additional features: users are able to pair public as well as private cloud storage buckets, and access cloud paths as if they were local filesystem paths.
-
- Standard Linux tools and other binaries are able to work with cloud paths when PetaLink is enabled. Here we described how the standard Linux cp command works with cloud paths, and that the transfer is accelerated when compared with the AWS CLI copy tool.
-
- Furthermore, HISAT2 is able to read input files located in the cloud. This means users avoid the need to first download the data to an instance. It also reduces the amount of storage space required on an instance and allows users to directly stream data from the cloud.
Overall, at PetaGene we have architected our compression solution to ensure data integrity, interoperability with all tools and pipelines through transparent decompression, and support for cloud storage to help reduce costs of cloud computing.
